| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 생활코딩
- 체크인미팅
- EC2
- Redis
- CICD
- NAT gateway
- openAI API
- 프리티어
- 인프라
- 프롬프트엔지니어링
- 게임개발동아리
- UNIDEV
- bastion host
- springai
- 라피신
- 티스토리챌린지
- 42서울
- Route53
- 전국대학생게임개발동아리연합회
- Spring boot
- 오블완
- 도커
- AWS
- 스프링부트
- 프로그래밍
- UNICON2023
- 백엔드개발자
- 개발공부
- 캡스톤디자인프로젝트
- UNICON
- Today
- Total
Hyun's Wonderwall
[정보통신공학] Chap 6. Error Detection & Correction 본문
Types of Errors
에러: TX와 RX 사이에 bit이 바뀐 것
- Single bit errors: 1개 bit가 바뀌고 주변에 영향x(isolated). white notse로 인해 발생할 수 있음.
- Burst errors: B 비트의 연속 시퀀스(첫 비트와 마지막 비트 및 그 중간 임의의 비트가 오류). 임펄스 노이즈 또는 모바일 무선 환경의 fading으로 발생 가능. 데이터 전송 속도가 높을수록 burst error의 영향이 커진다. (특정 시간동안 에러가 발생했을 때 깨지는 bit 수가 많음) (예시 그림을 보면 burst error of length B=10)
Error Control
• 디지털 전송 시스템에서 에러가 발생한다. BER: 에러 발생 확률.
- 구리선의 BER=10^(-6).
- 광섬유의 BER=10^(-9).
- 무선 전송의 BER=10^(-3) // 무선이 높다.
• 애플리케이션들은 특정한 신뢰성 수준을 요구한다.
- Data 앱: 에러 없이 전송해야 (error-free)
- Voice&Video 앱: 일부 오류 허용 (tolerate)
• Error Control은 전송 시스템이 애플리케이션 요구 사항을 충족하지 못할 때 사용된다.
• Error Control은 에러에도 불구하고 data stream이 특정 수준의 정확도로 전송되도록 보장한다.
Error Control Approaches 오류 제어 접근 방식
• Error Detection & ARQ
- RX는 에러를 감지하고 에러가 감지되면 TX에게 Automatic Retransmission Request(ARQ)를 보낸다.
- 재전송 요청을 위해 return channel이 필요하다. (sender가 보내는 채널이 channel. return channel은 반대로)
• Forward Error Correction (FEC, 전방오류수정)
- sender는 redundant data(a.k.a. error correction code)를 메시지에 추가함. 이것은 receiver가 sender에게 추가적인 데이터를 요구할 필요 없이 (일부 한계 내에서) 에러를 감지하고 정정할 수 있게 함.
- 한번에 더 많은 정보 보냄. 더 높은 대역폭이 요구되나, return channel이 필요하지 않거나 데이터의 재전송을 피할 수 있는 장점.
- 재전송이 상대적으로 비용이 많이 들거나 불가능한 상황에서 적용: 위성 및 심우주 통신; 오디오/비디오 CD 녹화
Key Idea of Error Detection
• 전송되는 모든 codewords은 패턴을 만족한다.
• 수신된 codewords가 패턴을 만족하지 않으면 에러.
• Redundancy: 전송을 위해 요구되는 추가적인 정보 (parity를 보내든 뭐를 보내든 추가적인 정보 필요)
• BlindSpot: 코드워드가 다른 코드워드로 바뀌어서 에러를 잡아내지 못하는 경우
[ User information -> Encoder -> Channel -> Pattern checking -> information 전달하거나 set error alarm ]
Error Detection Process
TX가 계산해서 붙이고, RX가 계산한 것을 비교.
- info k bits, parity bit이 n-k bits -> codeword n bits
- overhead: n-k/n
- parity bits = check bits = redundancy data
Checkbits & Error detection
- TX가 information k bits 이용해 check bit를 계산(n-k bits) -> Channel로 codeword n bits를 전송 -> RX가 받은 information bits로 check bits 다시 계산, 받은 check bits와 비교. 맞다면 정보 수락.
1. Parity
1. (1) Single Parity Check
- Info k bits에 Parity Bit 1 bit 연결 -> Codeword는 k+1bits.
- Parity Bit 계산: Info bits 다 더하고 mod 2
- 모든 codeword는 짝수개의 1을 가짐. Codeword 다 더하면 0인지 확인.
- 홀수개로 발생한 에러 감지 가능.(1이 홀수개) 그러나 짝수개 에러는 감지 불가.
- overhead: 1/(k+1)
* Single Parity Check code 얼마나 좋아?
- Redundancy: overhead 작다 (parity bit 1개)
- Covrage: 50%밖에 감지불가
- Redundancy와 Coverage는 서로 trade off
* What is a good code?
• 좋은 코드는 Codewords를 골고루 분산시켜야함. well-spread
- codewords가 서로 붙어있으면 감지 실패가 발생 (통신 채널에서 한 코드워드를 다른 코드워드로 잘못 인식하는 확률 높)
* What if bit errors are random?
- 1bit 에러 발생 확률 p (p < 0.5)
- P[10000000] = p * (1-p)^7 = p^2 * (1-p)^6
> P[11000000] = p^2 * (1-p)^6 = p * (1-p)^6 * (p/(1-p))
- p/(1-p) < 1 이므로 앞에서부터 두개 깨질 확률이 하나 깨질 확률보다 작음
- 하나의 에러를 갖는 패턴이 더 많
* Single parity check code with random bit error
- 감지 못하는 패턴: 짝수개 에러가 발생
P[감지실패] = P[감지못함] = P[1이 짝수개인 에러패턴]
= nC2*p^2*(1-p)^(n-2) + nC4*p^4*(1-p)^(n-4) + ....
- 예시: n=32, p=10^(-3)이라고 하자
P[undetectable error] = 32C2*(10^(-3))^2*(1- 10^(-3))^30 + 32C4*(10^(-3))^4(1- 10^(-3))^28 + ...
= 496 * 10^(-6) + 35960 * 10^(-12) + ... = 0.000496
- 이 예시에서는 약 1/2000의 에러 패턴이 undetectable하다
1. (2) Two Dimensional Parity Check
coverage 향상을 위해 더 많은 parity bit
• information을 열로 배열한다
• 마지막 열로 "parity"열을 붙이고 각 열의 끝에 단일 parity bit을 붙인다.
- 각 행과 열 별로 information bits를 XOR 계산해 parity bit 값을 구한다.
- 오른쪽 아래 끝 parity는 모든 info bits를 XOR한 값.
* Error-detecting capability
- 1~3개 에러는 항상 감지. 행 2개, 열 2개로 에러가 4개 발생시 감지 불가능
- 예시의 overhead: 10/30=1/3 (큼)
Other Error Detection Codes
- single parity check는 충분한 수의 에러를 감지 못하고 two-dimensional은 너무 오버헤드 큼.
- 실제로는 Internet Checksum과 CRC Polynomial Codes를 사용.
2. Internet Checksum
• 여러 인터넷 프로토콜(예: IP, TCP, UDP)은 check bits를 사용해 IP 헤더(또는 TCP/UDP에 대한 헤더 및 데이터)의 오류를 탐지.
• 헤더에 Checksum 필드가 있다. Checksum은 헤더 내용에 대해 계산된다.
• 모든 라우터에서 Checksum을 재계산한다. (헤더 내용에 문제가 없는지 확인. IP까지 까볼 수 있으니.) (hop to hop)
• 체크섬 계산:
- 헤더의 내용 부분이 L개의 16bit word로, 즉 b0, b1, ..., bL-1로 구성되어있다.
- 알고리즘으로 체크섬 bL을 계산. (checksum 길이=1 word 길이)
- 총 헤더 길이는 (L+1)*16bits, 오버헤드: 1 / (L+1)
* Checksum 계산
각 word가 16-bit word.
• x = (b0 + b1+ ... + bL-1) mod (2^16 - 1)
• bL = -x mod (2^16 - 1)
• codeword: (b0, b1, ..., bL)
• 0 = (b0 + b1+ ... + bL-1 + bL) mod (2^16 - 1)
RX가 코드워드 다 더해서 mod 계산했는데 0이면 에러 x
(2^16 - 1인 이유: 1111 1111 1111 1111)
* 예제
4-bit words였다면, 2^4 - 1 = 15. mod 15.
10000 mod 15 = 0001.
- codeword: (b0, b1, b2) -> (1100 1010 1000)을 codeword로 보낸다
- 1의 보수
3. Polynomial Codes
• bits를 다항식의 계수로 연산.
• shift-register-circuit으로 구현된다.
• CRC(Cyclic Redundancy Check) codes 라고도 불린다
• 대부분의 에러 감지에서 이 방법을 사용. error corredtion에서도 사용함.
- CRC는 데 이터의 끝에 붙여지는 형태로 전송된다. 데이터의 무결성을 보장하기 위한 추가 정보.
Cyclic Reduncdancy Check (CRC)
- D: data bits (주어짐)
- G: Generator. CRC 코드를 만드는 기반이 되는 비트 패턴. r+1 bits (주어짐)
- R: CRC bits. r bits (Generator보다 1bit 작음)
목표: <D,R>을 G으로 나눈 나머지가 0이 되도록 하는 CRC bits(R)를 선택
- 전체 보내고자 하는 codeword: <D,R> = D*2^r XOR R.
- D가 d bits, R이 r bits였다면 codeword는 d+r bits.
- CRC bits 구하기: R = D * 2^r / G. data bits를 shift left r 하고 G로 나눔. (*나누는 것은 mod 2)
• 수신기는 G를 알고 있고(circuit) <D,R>을 G로 나눈다. 0임: 에러x, 0이 아님: 에러 감지!
• r+1비트 미만의 모든 burst error를 감지 가능.
• 실제로 널리 사용된다 (이더넷, 802.11 WiFi)
- 예제
D: 101110, G: 1001.
R = remainder [ D * 2^r / G ] // r bits.
R가 011 나옴. 보내는 코드워드: (101110011).
코드워드/G -> 나머지 0
Binary Polynomial Arithmetic
binary vector들을 다항식으로 대응시킴
덧셈은 mod 2
비트 계산 더 편함
Polynomial Coding
- Codeword = x^(n-k) * i(x) + r(x)
- Codeword n bits = info k bits + remainder n-k bits
Codeword 다항식 차수는 n-1
Info bits i(x)의 차수는 k-1 // x^(n-k) * i(x)는 비트 시프트 한 것
Generator g(x) 차수는 n-k: g(x) = x^(n-k) + g_(n-k-1)*x^(n-k-1) + ... + g_2*x^2 + g_1*x +1
remainder 차수는 n-k-1
x^(n-k) * i(x) = q(x)*g(x) + r(x).

예시
g(x) = x^3 + x + 1 (1011)
i(x) = x^3 + x^2. // k = 4
g(x)가 4bit이기 때문에 CRC=3bits. 따라서 codeword 길이 n=7bits.
i(x)를 왼쪽으로 3bit 밀어서 *x^3임.
(나누는 과정에서 XOR 처럼 하는 것은 동일함)
r(x) remainder가 x -> CRC: (010)
The pattern in polynomail coding
RX가 g(x)로 나눴는데 zero면 문제x, nonzero면 문제o
Standard Generator Polynomials
Generator 비트 패턴은 공개된다. 아래는 표준들.
CRC-8: x^8 + x^2 + x + 1이 G
CRC-16: x^16 + x^15 + x + 1
(CRC) CCITT-16: x^16 + x^12 + x^5 + 1 // HDLC 등
(CRC) CCITT-32 = x^32 + x^26 + x^23 + ... // IEEE 802 등
G_CRC-32 = 위의 다항식이 이진수
Basic ARQ with CRC
Packet sequence를 -> Transmitter가 보냄 (Station A)
-> Information frames이 TX에서 RX로 보내짐 (Channel 통해)
-> Receiver가 받고 (Station B), Header, CRC 써서 에러 detection함
-> 에러 있으면 Return Channel을 통해 RX가 TX로 control frame를 다시 보냄
/ 에러 없으면 패킷을 사용
Information Fram: Header + Information packet + CRC
Control frame: Header + CRC
End-to-End vs. Hop-by-Hop
- Error Control 어디서? 두가지 방법. 트레이드오프가 존재.
1) end-to-end: 전체적으로 못받은 것 없는지 확인. 소스와 목적지 사이에서만 에러 컨트롤
2) Hop-by-Hop: 네트워크의 모든 기기에서 에러 컨트롤
Data Link Layer의 Error Control
• Data Link는 유선과 같은 직접 연결된 시스템을 통해 작동한다.
- 이웃한 것들 간에 Frame이 Medium을 통해 오간다 (hop-by-hop)
• 프레임이 손상되거나 손실될 수 있지만 순서대로 도착한다.
• Data Link가 오류 확인 및 재전송을 수행. 오류 없는 패킷 전송을 보장한다.
Transport Layer의 Error Control
• TCP는 네트워크 간에 segment를 전송하고 end-to-end 에러 검사 및 재전송을 수행한다.
• 네트워크가 신뢰할 수 없는 것으로 가정.
• 세그먼트는 긴 지연을 경험하거나 손실되거나 순서에 맞지 않게 도착할 수 있다.
• End-to-end 프로토콜이 더 어렵다.
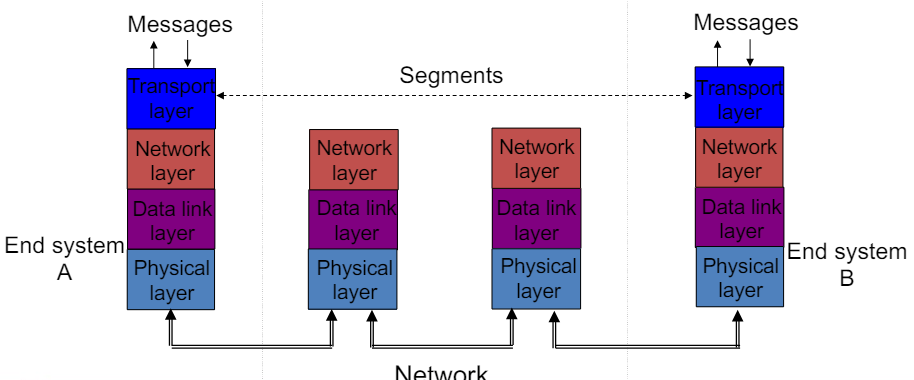
End-to-End Approach Preferred
- Hop-by-Hop은 End-to-End 완전성을 보장하지 못함. 장점은 에러 발생시 빠른 복구 가능.
- End-to-End는 네트워크 내부가 심플함. 데이터 완전성 보장함. 확장성 높음.
- ACK/NAK는 긍정 응답/부정 응답
'Subjects > 정보통신공학' 카테고리의 다른 글
| [정보통신공학] Week 13-14. Ethernet (0) | 2024.06.12 |
|---|---|
| [정보통신공학] Chap 7. Data Link Protocols (0) | 2024.04.21 |
| [정보통신공학] Chap 5. Data Encoding, Modulation, Sampling 및 Quantization (0) | 2024.04.19 |
| [정보통신공학] Chap 4. Transmission Media (0) | 2024.04.19 |
| [정보통신공학] Chap 3. Data Transmission (0) | 2024.04.19 |


