| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 자바개발자
- EC2
- Developer
- 체크인미팅
- 오블완
- 프로그래밍
- 스프링부트
- 개발공부
- 도커
- 배포
- 티스토리챌린지
- 생활코딩
- 백엔드
- 42서울
- UNIDEV
- 전국대학생게임개발동아리연합회
- 스프링
- 인프라
- AWS
- 인디게임
- 라피신
- CICD
- 위키북스
- 온라인테스트
- UNICON
- UNICON2023
- 백엔드개발자
- RDS
- 게임개발동아리
- 프리티어
- Today
- Total
Hyun's Wonderwall
[컴퓨터알고리즘] 10. 이진검색트리 본문
Binary Search Tree (BST, 이진검색트리)
- 동적 집합 연산을 지원하는 자료구조. (search, minimum, predecessor, successor, insert, delete)
- 수행시간이 트리의 높이에 비례: O(h)
- 한 노드의 왼쪽, 오른쪽 자식노드도 각 서브트리의 루트가됨 -> 재귀적으로 이진탐색트리
- 노드들이 연결된 자료구조.
- root(T)가 T의 루트노드를 가리킨다. // p[root[T]]=NIL
- null도, 노드가 1개여도 BST이다.
- 각 노드가 포함하는 필드들: key, left(왼쪽 자식 노드의 포인터), right(오른쪽 자식 노드의 포인터), p(부모 노드의 포인터), satellite data(부속 데이터)
- 루트 노드는 부모노드가 NIL인 유일한 노드. 자식노드 없으면 해당필드 NIL값.
BST 특성 (반드시 모두 만족시켜야)
- x의 왼쪽 서브트리에 있는 모든 y는 key[y]<=key[x]여야 한다.
- x의 오른쪽 서브트리에 있는 모든 y는 key[y]>=key[x]여야 한다.
Inorder Traversal 중위순회
- BST 중위순회 -> 재귀적으로, key값 증가하는 순서로 출력 (=오름차순 정렬 결과.)
Inorder-Tree-Walk(x)
if x != NIL
then Inorder-Tree-Walk(left[x])
print key[x]
Inorder-Tree-Walk(right[x])
- 시간복잡도 Θ(n) 증명
InOrder(x)가 시간복잡도 Θ(n)를 갖음을 보여라.
n개노드 모두 방문해야 하기 때문에 T(n)=Ω(n)이다. T(n)=O(n)을 보이면 된다.
1) 빈 트리 (x!=NIL) -> 경미한 상수 시간이 걸리므로 c>0에 대해 T(0)=c이다.
2) n>0인 경우, 왼쪽 서브트리가 k개 노드를 갖고 오른쪽 서브트리가 n-k-1개 노드를 가지면
T(n) <= T(k)+T(n-k-1)+d, d>0은 InOrder(x)를 수행하는데 재귀호출에 걸리는 시간 외의 상한을 반영한다.
T(n)=O(n)를 보이기 위해 치환법을 사용한다. T(k)=(c+d)k+c로 놓자.
T(n) <= (c+d)k+c + (c+d)(n-k-1)+c + d
= (c+d)n + (c-c-d+c+d) = (c+d)n + c
따라서 T(n)<=cn 이므로 T(n)=O(n)이다.
Tree Search 이진탐색트리 탐색
- 시간복잡도: O(h)
Tree-Search(x,k)
if x=NIL or k=key[x] # 끝이거나 찾았다면 x 반환
then return x
if k<key[x]
then return Tree-Search(left[x], k) # k<key[x]면 왼쪽에 있음
else return Tree-Search(right[x], k) # k>key[x]면 오른쪽에 있음
Iterative Tree Search 반복문으로 찾기
- 반복문으로 찾는 게 재귀보다 더 효율적!!
Iterative-Tree-Search(x,k)
while x!=NIL and k!=key[x] # x가 NIL이 아니며 k를 찾지 못한 동안 반복한다
do if k<key[x]
then x<-left[x] # k<key[x]면 왼쪽 탐색
else x<-right[x] # k>key[x]면 오른쪽 탐색
return x # x 반환
Finding Mix&Max 최댓값/최솟값 찾기
- min은 왼쪽 제일끝, max는 오른쪽 제일끝. // 주의: while조건이 x가아니라 left[x] != NIL / right[x] != NIL이다.
- 시간복잡도 O(h)
Tree-Minimum(x)
while left[x] != NIL
do x <-left[x]
return x
Tree-Maximum(x)
while right[x] != NIL
do x <-right[x]
return x
Predecessor 직전원소, Successor 직후원소
- 직후원소: key[x]이상인 key들 중 최솟값 key를 갖는 노드 y. (바로 오른쪽.)
- 어떤 노드의 다음 key값을 찾아야 할 때 사용. (삭제연산 등)
- 최대원소의 직후원소는 NIL.
직후원소 찾기 - 두 가지 경우
1. 노드 x가 비어 있지 않은 오른쪽 서브트리를 가지고 있는 경우
- x의 직후원소: x의 오른쪽 서브트리에서 최솟값 키를 갖는 노드
2. 노드 x가 비어 있는 오른쪽 서브트리를 가지고 있는 경우
- x의 직후원소: x의 조상이면서 왼쪽 자식도 x의 조상인 가장 낮은 조상 노드
(왼쪽으로 올라가다 오른쪽으로 최초 1번 올라온 순간의 노드)
Successor 직후원소 수도코드 - 다 right를 사용한다.
// Predecessor도 작성해보기 - 다 left
- 시간복잡도 O(h). 트리의 높이가 어떤 한 값으로 고정되지 않음. (lg n<=h<=n.)
Tree-Successor(x)
if right[x]!=NIL
then return Tree-Minimum(right[x])
y<-p[x]
while y!=NIL and x=right[y]
do x<-y
y<-p[y]
return y(1) right[x] != NIL 일 때 -> Tree-Minimum(right[x])의 반환값을 리턴한다. (x의 오른쪽 서브트리의 최솟값)
(2) right[x] == NIL일 때 -> y가 NIL이거나 x != right[y]면 빠져나옴 (즉, x=left[y]), y를 반환한다.
- while문에서는 x에 y를 저장하고 y에 y의 부모노드를 저장한다 (이때 x는 y의 자식노드)
BST 삽입 Tree-Insert(T,z)
- 삽입 후에도 BST 특성이 보장되어야 한다. NIL이 있던 자리에 z를 삽입한다.
- 주의할점: x를 돌린후에 y가 NIL인지를 체크해야한다.
Tree-Insert(T, z)
y<-NIL # y는 이제 x의 부모노드 역할이다
x<-root[T] # 트리 루트부터 시작
while x!=NIL # x가 NIL되면 탈출
do y<-x # y에 x 저장
if key[z]<key[x] # z, x key값 비교
then x<-left[x] # x에 x의 왼쪽 자식원소 저장
else x<-right[x] # x에 x의 오른쪽 자식원소 저장
p[z]<-y # z의 부모 y에 저장
if y=NIL # y가 NIL인 경우는 빈 트리, z를 y에 연결하지x
then root[t]<-z # z가 root가 된다
else if key[z]<key[y] # z와 y 비교해 y의 왼/오 자식 결정
then left[y]<-z
else right[y]<-z
Tree-Delete(T,x) 트리 삭제
case 0: 자식 0개 -> x 삭제
case 1: 자식 1개 -> x 삭제하고 p[x]가 자식 가리키게함
case 2: 자식 2개 -> x를 successor와 바꾸면 case0/1되므로 그에 따라 삭제
시간복잡도 O(h)
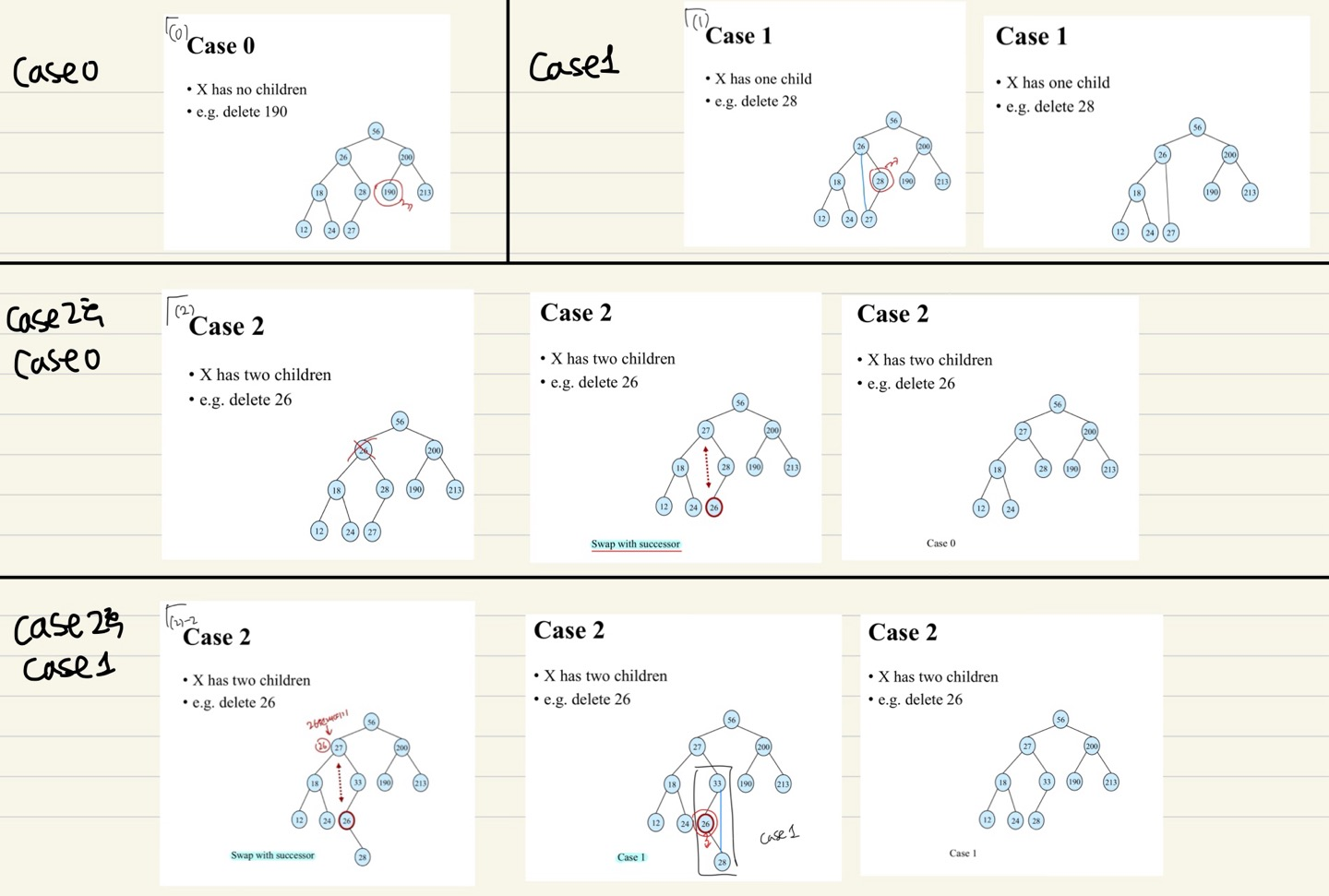
Tree-Delete의 Correctness
- 어떻게 case 2 이후에 case 0/1? successor는 x이상인 값 중 최솟값이므로 왼쪽 자식노드가 없음 -> 0/1개 자식노드
BST 삭제 Tree-Delete(T,z)
Tree-Delete(T,z)
if left[z] = NIL or right[z] = NIL
then y <- z # case 0 또는 1 - z의 자식이 0/1개, y는 z
else y <- Tree-Successor[z] # case 2 - z의 자식 2개, y는 직후노드(right[z], 자식 0/1개)
# x에 y의 (non-NIL)자식노드나 NIL을 담음 (y의 자식노드는 0/1개)
if left[y] != NIL
then x<-left[y]
else x<-right[y]
# x가 존재하면(y의 자식노드), x가 부모로 y의 부모노드를 가리키게 함.
if x != NIL
then p[x] <- p[y]
# p[y]와 x의 포인터를 조작하여 y를 tree에서 빼기
if p[y] = NIL # p[y]가 NIL이라면 y가 root라는 뜻이고, y부모와 연결할필요x
then root[T] <- x
else if y = left[p[y]] # y가 y부모의 어떤자식이었는지(왼/오) 확인하고 x 연결
then left[p[y]] <- x
else right[p[y]] <- x
# z의 successor가 잘렸으므로 z에 y의 data를 복사한다
if y != x
then key[z] <- key[y]
copy y's satellite data into z
return y
Querying a Binary Search Tree
첫 키가 root, 걔를 기준으로 왼?오? 결정됨.
- 모든 동적 집합 탐색 연산은 O(h) 시간 소요.
- 균형 이진 탐색 트리: Θ(lgn), 불균형트리: Θ(n)
'Subjects > 컴퓨터알고리즘' 카테고리의 다른 글
| [컴퓨터알고리즘] 12. 동적 프로그래밍 (0) | 2024.06.20 |
|---|---|
| [컴퓨터알고리즘] 11. 레드블랙트리 (0) | 2024.06.19 |
| [컴퓨터알고리즘] 5장 - 힙 정렬 (0) | 2024.04.24 |
| [컴퓨터알고리즘] 4장 - (2) 분할정복기법 (0) | 2024.04.24 |
| [컴퓨터알고리즘] 4장 - (1) 점화식 (0) | 2024.04.24 |

