| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- EC2
- 티스토리챌린지
- 라피신
- 인프라
- AWS
- bastion host
- 프로그래밍
- NAT gateway
- 게임개발동아리
- VPC
- CICD
- UNICON2023
- 42서울
- 전국대학생게임개발동아리연합회
- 자바개발자
- UNIDEV
- 프리티어
- 개발공부
- 온라인테스트
- 인디게임
- 위키북스
- 오블완
- 백엔드개발자
- 스프링부트
- 체크인미팅
- 도커
- 백엔드
- 생활코딩
- UNICON
- Route53
- Today
- Total
Hyun's Wonderwall
[컴퓨터알고리즘] 12. 동적 프로그래밍 본문
12.1
동적 프로그래밍(DP): 격자(배열) 만들어 사용
- 분할정복 DAC와의 비교: 문제를 부분 문제로 나누어 해결하는 것이 비슷.
- DAC는 하위 문제들이 서로 독립적, DP는 서로 연관.
- 하위 문제들이 겹침 -> DAC는 중복 계산하지만 DP는 table에 저장하는것으로 단 1번만 계산.
DP 알고리즘 수립
1. 최적해의 구조 특징을 찾는다.
2. 최적해의 값을 재귀적으로 정의한다.
3. 최적해의 값을 상향식(bottom-up)으로 정의한다.
4. 계산된 정보들로부터 최적해를 구성한다.
DP 알고리즘의 구성요소
1. Optimal sub-structures 최적의 하위구조
2. Overlapping sub-problems 겹치는 부분문제
3. Memoization and reuse 메모이제이션과 재사용
Optimal sub-structures 최적의 하위구조
- 문제 크기 n일때, 하위구조인 n보다 작은애들도 최적이라는것.
Overlapping sub-problems 겹치는 부분(하위)문제
- 문제를 겹치지 않는 하위문제들로 분할한다 -> 같은 argument로 여러번의 재귀가 발생한다.
ex. 피보나치: F(n)=F(n-1)+F(n-2) (n>2), F(1)=F(2)=1
피보나치
1) 재귀적인 방법: 시간복잡도 O(2^n/2 ~ 2^n) = O(1.6^n) 안좋음.
2) 반복적인 방법: 훨씬좋음! (c, p, pp)
function fib(n)
a = 1, b = 1;
if (n==1||n==2) return 1;
for i=3 to n
c = a + b;
a = b;
b = a;
return c;3) DP로 풀기: 메모이제이션(재귀) / 배열(반복)
역들간의 최소비용
N(0 ~ N-1) 개의 기차역이 기차 경로에 있다. 0->1->2->...->N-1 으로 연결되어있다.
int cost[N][N] = { 4x4 2차원배열 }; # cost[a][b]: a->b 직행으로 가는 비용
minCost(0, N-1) # 0에서 N-1까지 이동
= MIN { cost[0][N-1], cost[0][1]+minCost(1,N-1), minCost(0,2)+minCost(2,N-1), ..., minCost(0,N-2)+cost[N-2][N-1] }
// 인접해서 간격이 1인 경우만 cost[a][a+1]을 활용할 수 있고 그외엔 minCost(a,b)로 구해야 한다
minCost(0, N-1) 의사코드
function minCost(s,d)
if (s==d || s==d-1)
return cost[s][d];
minValue = cost[s][d]; # 직행 요금 저장
for i = s+1 to d-1
temp = minCost(s,i) + min(i,d);
if (temp < minValue)
minValue = temp; # 최소 요금 갱신
return minValue;지수 시간 연산 필요. optimal, overlapping한 특징 확인 가능
Memoization 메모이제이션
문제를 재귀적으로 풀되, 중복되는 계산을 피하기 위해 결과를 저장함..
( func(n): 계산한 문제인지 확인 -> 메모리에 값 있으면 메모리에서 결과 가져와서 반환, 메모리에 값 없으면 n에 대한 하위 문제 계산한 후 결과를 메모리에 저장한후 다시 꺼내서 반환)
메모이제이션으로 피보나치
- 일차원 배열에 다 저장 -> 재귀로 인해 지수시간(안좋음)
memo[N] = {0};
function fib(n)
if (memo[n] != 0) # memo[n]에 값이 있으면 바로 반환
return memo[n];
if (n==1 || n==2)
memo[n] = 1;
else
memo[n] = fib[n-1] + fib[n-2]; # 재귀적이어야함
return memo[n];
Memoization: minCost
memo[N}[N} = {0}; # 2차원 배열
function minCost(s,d)
if (s==d || s==d-1)
return cost[s][d];
if (memo[s][d] == 0)
minValue = cost[s][d];
for i = s+1 to d - 1 # 반복문
temp = minCost(s,i) + minCost(i,d); # 재귀적인 부분
if (temp < minValue)
minValue = temp;
memo[s][d] = minValue;
return memo[s][d];* 단점: O(n^2) 추가 공간 필요, 시간복잡도 O(n^3)
minCost(s, d)는 for문 1개에서 O(n)의 시간복잡도를 가짐.
전체 DP 테이블은 O(n^2)개의 부분 문제 가짐 (각 부분 문제가 O(n) 시간에 해결됨)
=> 따라서 전체 시간복잡도는 O(n^3).
// Memoization은 여전히 재귀호출적인 방법. (재귀 +cache -겹치는부분문제)
Dynamic Programming
* Top-Down Dynamic Programming: memoization (메모이제이션)
- 재귀적 접근: 문제를 더 작은 하위 문제로 나눠서 재귀적으로 해결해.
- 메모이제이션: 이미 계산한 하위 문제의 결과를 저장해두고, 동일한 하위 문제가 다시 나타날 때 저장된 값을 이용해 중복 계산을 피함.
* Bottom-Up Dynamic Programming: Tabulation (테이블화) (보통 DP하면 상향식 떠올림)
- 반복적 접근: 작은 문제부터 해결하면서 차례대로 큰 문제를 해결.
- 테이블화: 하위 문제의 결과를 테이블(배열)에 저장하고, 이를 이용해 상위 문제를 해결.
DP로 피보나치
- arr[n+1] 배열 만들어 사용 (arr[0] 안쓰기위해)
- 반복문을 통해 arr[k]에 f(k) 결과가 담긴다. 재귀가 없어 오버헤드 적다!
function fib(n)
int arr[n+1];
arr[1] = 1;
arr[2] = 1;
for i = 3 ot n
arr[1]=arr[i-1]+arr[i-2];
return arr[n];
DP로 역들간의 최단경로
function minCost(N)
minValue[N]; # N 크기의 배열
minValue[0] = 0;
minValue[1] = cost[0][1];
for i=2 to N-1
minValue[i] = cost[0][i]; # minValue[i]를 구해야 한다
for j=1 to i-1
# minValue[j] + cost[j][i]들과 비교해서 최솟값으로 갱신한다
if (minValue[i] > minValue[j] + cost[j][i])
minValue[i] = minValue[j] + cost[j][i];
return minValue[N-1] # 인덱스 N-1의 원소가 N번째역의 원소12.2
0-1 Knapsack problem
- 가방 무게 W. 물건 1~n. 각각의 무게 w1~wn. 각각의 가치 v1~vn.
- 목적: wi합<=W이고, vi합이 최대인 subset S 구하기
cell[i][j] = { (1)이전 최댓값 cell[i-1][j] vs (2) 현재물건가치+남은무게채우는물건의가치 } 를 비교, 최댓값 계산
cell[i번째물건까지확인][무게] = 가치
ex) cell[3][4] = 20 + cell[3][4-3]
격자 다 채웠을 때 맨 오른쪽 하단이 정답
4kg 가방 MAX value? A(1kg, 15$) + C(3kg, 20$) = 35$
Case 1: item n을 가방에 넣음 -> W-wn의 무게 남음
Case 2: item n을 가방에 넣지 x -> W의 무게 남음
재귀적 함수로 knapsack문제
V[i,j] = max(V[i-1, j], // item i안넣음
V[i-1, w-wi] + vi) // item i 넣음
fuction knapSack(W[], V[], n, w)
for (i=0 to n)
grid[i][0] = 0; # 0번째열 원소 모두 0으로
for (j=0 to w) # w는 가방 최대 무게
grid[0][j] = 0; # 0번째행 원소 모두 0으로
for (i=1 to n)
for (j=1 to w) # j는 열 (무게)
if (W[i-1] <= j) # i번째 아이템의 무게 W[i-1]<= j 일 때
x = j - W[i-1]; # x는 남은 무게
grid[i][j] = MAX(grid[i-1][j], V[i-1]+grid[i-1][x]);
else
grid[i][j] = grid[i-1][j];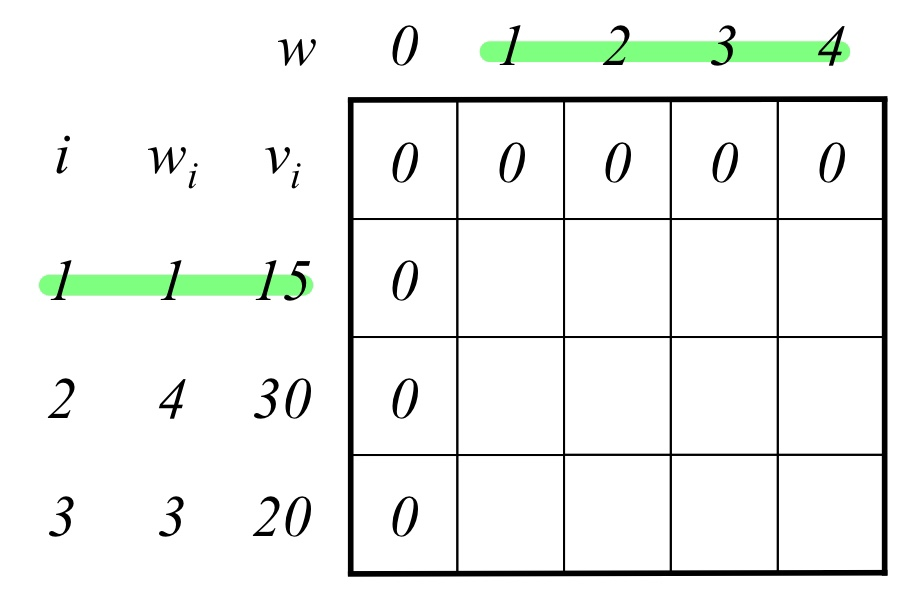
Sub-String Problem 부분 문자열 문제
주어진 문자열에서 a|a' 나눴을 때 a, a' 숫자합이 같은 최대 길이의 부분 문자열 aa'를 찾는다. (합친문자열)
Input: "142|124" "1|1"25 9"43|07"26
Output: 6 2 4
for문 3번 -> 시간복잡도 O(n^3)
for (i=0 to n-1)
for (j=i+1 up+2 n-1) # 두개씩 넘김 (문자열 길이 짝수여야)
len = j - i + 1; # 문자열 길이
int lSum = 0, rSum = 0; # 왼쪽합, 오른쪽합 계산
for (int k=0; k<len/2; k++) # k를 반복자로 사용
lSum += (str[i+k] - '0'); # i+k에서 시작
rSum += (str[i+k+len/2] - '0'); # i+k+len/2에서 시작
# lSum과 rSum이 같다면 maxLength 갱신
if (lSum == rSum)
maxLength = len;
return maxLength;
i = 0 -> j = 1, 3, 5 -> len 2, 4, 6
i = 1 -> j = 2, 4, 6 -> len 2, 4, 6
...
Sub-String Problem
1) length가 1: S(i,i)
2) length가 2: S(i,j)=S(i,i)+S(j,j)
3) length가 3: 1 + 2
* S(i, j) = i번째 부터 j번째 까지 숫자의 합
* S(i, j) = S(i, k) + S(k+1, j) # 일반화한 식
overlapping sub-problem 존재함. 반복계산 多 -> 문제를 잘게 잘라야함.
sum[i][j]에 i부터j까지 숫자합을 적는다. 최댓값이 x. 부분 문자열 최대 길이는 maxLength 변수에 저장.
maxSubString 수도코드
function maxSubString(str)
n = strlen(str);
maxLength = 0;
for (i=0 to n-1) # 초기화
sum[i][i] = str[i] - '0';
for (len=2 to n) # len은 길이 (2 이상~n)
for (int i = 0; i < n - len + 1; i++) # i는 시작 인덱스
j = i + len - 1; # j는 끝 인덱스
k = len/2;
sum[i][j] = sum[i][j-k] + sum[j-k+1][j];
if (len % 2 == 0 && sum[i][j-k] == sum[j-k+1][j] && len > maxLength)
maxLength = len;
return maxLength;순서
1) len = 1 인 경우가 str[i] 이므로
sum[i][i] = str[i] - '0'; 해주기 (sum은 i~j의 합을 저장하는 이차원배열)
2) len = 2 to n
sum[i][j] = sum[i][j-k] + sum[j-k+1][j] 문자열 합 쓰는것 반복
최대 길이 부분문자열 저장하는것은 maxLength에서 진행함.
다이내믹 프로그래밍 기본 전략
1) 재귀 호출
- 여기에서 처리하는 문제해결기법을 그대로 DP에 적용. (순환x 반복적인 방법으로 개선.)
- 먼저 재귀호출로 풀어본 후 메모이제이션이나 DP 활용/
2) 메모 전략: 재귀o, 하위문제 중복계산 피하기
3) DP 상향식: 재귀x, 반복
12.3
Sequence alignment 시퀀스 정렬
- 두 문자열을 비교해 유사성을 본다.
- Longest Common Subsequence problem (LCS)
Common subsequence 공통 부분시퀀스
- 문자열의 '부분시퀀스'는 그 시퀀스에서 0개 이상의 char를 뺀 문자열을 말한다.
- ex. 문자열 x = {ABCBDAB}, y = {BDCABA} . x와 y의 공통 부분시퀀스는 {BC}, {BDA}, {BCBA} 등이 있다.
Longest Common Subsequence 최장 공통 부분시퀀스
- 두 시퀀스 x[1..m]과 y[1..n[이 주어질 때, 둘 사이의 최장 공통 부분시퀀스 하나를 구한다 (유일x)
- 위의 경우엔 BCBA = LCS(x,y)
- 브루트포스로 LCS 알고리즘을 계산하면 지수형 시간복잡도 (안됨!!)
LCS의 최적 부분구조
- 정의: X_{i}는 X의 i번째 prefix(접두사)를 의미한다. X_{i} = <x1, x2, ..., xi>
- 예시: X = <A,B,C,B,D,A,B>에서 X_{4} = <A,B,C,B>이고 빈 시퀀스임. (공집합∅ 부분수열)
- 주어진 조건:
두 시퀀스 𝑋 = < 𝑥1 , 𝑥2 , … , 𝑥𝑚 > 와 𝑌 = < 𝑦1 , 𝑦2 , … , 𝑦𝑛 >
𝑍 = < 𝑧1 , 𝑧2 , … , 𝑧𝑘 >가 𝑋와 𝑌의 LCS라고 하자.
x, y 두 시퀀스의 마지막 문자가 같은지 다른지에 따라 케이스 2개로 나눔. => 재귀적 풀이, DP가능
Case 1: x_m = y_n
만약 x_m=y_n이라면, zk=xm=yn이고 Z_{k-1}은 X_{m-1}과 Y_{n-1}의 LCS가 됨.
-> LCS(X,Y) = LCS(X_{m-1}, Y+{n-1}) + x_m
Case 2: x_m != y_n
만약 x_m != y_n이고 z_k != x_m라면 는 X_{m-1}과 Y의 LCS가 됨.
만약 x_m != y_n이고 z_k != y_n라면 Z는 와 Y_{n-1}의 LCS가 됨.
-> LCS(X,Y) = max { LCS(X_{m-1}, Y), LCS(X, Y_{n-1}) }
Recursive thinking 재귀적인 관점에서 생각
* Case 1: x[m] = y[n]
LCS(x,y) = LCS(x[1..m-1], y[1..n-1]) || x[m]
// x, y, LCS 양쪽에서 1개 문자 빼고 x[m]을 이어붙임
- LCS의 길이 c[m,n] = c[m-1, n-1] + 1
* Case 2: x[m] != y[n]
Case 2.1: x[m]은 LCS에 없다 -> LCS(x[1..m-1], y[1..n]) 찾기
Case 2.2: y[n]은 LCS에 없다 -> LCS(x[1..m], y[1..n-1]) 찾기
LCS(x,y) = max { LCS(x[1..m-1], y[1..n]), LCS(x[1..m], y[1..n-1]) }
- LCS의 길이 c[m,n] = max { c[m-1,n], c[m,n-1] }
일반화: 재귀적 함수
c[i,j] = c[i-1,j-1] + 1 또는 max{c[i-1,j], c[i,j-1]} ( x[i]=y[i]인지에 따라)
LCS(x,y,i,j)
if x[i] = y[j]
then c[i,j] <- LCS(x,y,i-1,j-1) + 1
else c[i,j] <- max { LCS(x,y,i-1,j), LCS(x,y,i,j-1) }
Worst-case: x[i] != y[i] (재귀를 두 번 하므로)
남아있는 문자열 더이상 없으면 0을 리턴한다.
lcsLength c언어 코드
int lcsLength(char X[], char Y[], int m, int n)
{
if (m==0 || n==0) return 0;
if (X[m-1] == Y[n-1])
return 1 + lcsLength(X, Y, m-1, n-1);
else
return MAX(lcsLength(X,Y,m,n-1), lcsLength(X,Y,m-1,n));
}
재귀 트리 그려보면 겹치는 부분 문제들 생김. DP 알고리즘 쓰자
- 포인트: 부분 문제를 푸는 옳은 순서를 찾는 것
- 부분 문제의 총 갯수: m * n
테이블에서 c[i,j]를 보면 부분문제로 쪼갤 때 i->0, j->0
function lcsLength(X[], Y[], m, n)
int grid[m+1][n+1];
for i = 0 to m
grid[i][0] = 0;
for i = 0 to n
grid[0][j] = 0;
for i = 1 to m
for j = 1 to n
if (X[i-1] == Y[j-1]) # 주의: X[i-1]이 X의 i번째 원소
grid[i][j] = grid[i-1][j-1] + 1;
else
grid[i][j] = MAX(grid[i-1][j], grid[i][j-1]);
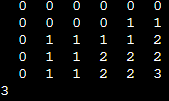
LCS 예시
- X=ABCB와 Y=BDCAB의 LCS는 BCB
순서
1) 각 길이 4, 5이므로 인덱스 4, 5까지 쓰기 위해 c[5,6] 할당
2) c[i,0]과 c[0,j] 0으로 값 초기화
3) 이중 for문 (바깥 i, 안쪽 j)
Xi와 Yj 같으면 1 더함
다르면 c[i,j] = max ( c[i-1,j], c[i,j-1] )
이를 통해 grid[m][n]에서 LCS 길이를 알 수 있다.
LCS 시간복잡도 O(m*n)
- 배열 c[m,n]의 모든원소 계산. c[i,j]는 상수시간에 계산됨
LCS 찾기: trace back. O(m+n)
- 현재값보다 왼쪽값 작으면 현재위치 char 이어붙이고 왼쪽위로 이동. 왼쪽값이 같으면 왼쪽으로 이동. 0 나올 때까지 힘.
- 얻게 된 문자열은 순서가 바뀌어있으니 뒤집어주어야함.
Rod cutting 막대 자르기
- 막대를 자른다. 막대길이마다 가격이 다르다. 여러가지 자르는 방법 확인하고 수입을 최대화해야함.
- 막대는 2^(n-1) 가지 방법으로 자를 수 있다.
n = i1 + i2+.. + ik (i는 길이)
r_n = p_i1 + p _i2 + .. + p_ik (r은 수입, p는 가격) (r_n은 n개를 잘랐을 때의 수입)
r_n = max (p_n, r_1+r_{n-1} + r_2 + r_{n-2} + ... + r_{n-1} + r_1)
주의 j가 바깥에 있음
- DP로 풀면 훨씬 간단. q = max(q, p[i]+r[j-1])
BOTTOM-UP-CUT-ROD(p,n)
let r[0..n] be a new array
r[0] = 0
for j = 1 to n
q = -무한대
for i = 1 to j
q = max(q, p[i]+r[j-1])
r[j] = 1
return r[n]
DP c언어 구현할 줄 알아야 함
#include <stdio.h>
#include <string.h>
# define MAX(a,b) ((a) > (b) ? (a) : (b))
int lcsLength(char X[], char Y[], int m, int n)
{
int grid[m+1][n+1];
for(int i=0; i<=m; i++)
grid[i][0] = 0;
for(int j=0; j<=n; j++)
grid[0][j] = 0;
for(int i=1; i<=m; i++)
for(int j=1; j<=n; j++)
if(X[i-1] == Y[j-1])
grid[i][j] = grid[i-1][j-1] + 1;
else
grid[i][j] = MAX(grid[i-1][j], grid[i][j-1]);
for(int i=0; i<=m; i++)
{
for(int j=0; j<=n; j++)
printf("%3d", grid[i][j]);
printf("\n");
}
return grid[m][n];
}
int main()
{
char X[30] = "ABCB";
char Y[30] = "BDCAB";
printf("%d\n", lcsLength(X, Y, strlen(X), strlen(Y)));
}
* 최소 비용 경로 문제: 통행세. 2차원 배열 비용 행렬 주어짐.
- (0,0)부터 해당칸까지 최소 비용 경로의 비용 담는 2차원 배열 만듬. (비용 행렬과 별도임! 주의)
- 오른쪽/아래쪽으로만 이동할 수 있을 때: min(왼쪽칸, 윗칸) + 비용[i,j]
- 우하향 대각선 방향까지 이동할 수 있을 때: min(왼쪽칸,윗칸,왼위대각선칸) + 비용[i,j]
* 편집 거리 문제: 두 문자열. 삽입/삭제/수정 (3개 중 하나 하는데 1의 비용이 듬)
* 연속 행렬 곱셈 문제: 행렬의 곱셈 순서를 최적화하여 곱셈 연산 횟수를 최소화하는 문제
- 행렬 A1 (10x20), A2 (20x5), A3 (5x15), A4 (15x30) 가 주어짐.
- 연속된 행렬 간의 곱셈이 가능. (A1*A2)*A3과 A1*(A2*A3) 계산횟수가 다름!
* 동적 계획법 접근
- 행렬 크기 배열 : [10, 20, 5, 15, 30] // A1~A4 행렬의 가로/세로 길이를 넣음 -> d0~d4, 거리로써 사용됨.
- 비용 행렬 : m[i][j]는 행렬 A_i에서 A_j까지의 최소 곱셈 연산 횟수를 저장
- 최적 분할 행렬 s: 최적의 곱셈 순서를 추적하기 위해 사용
* 초기화: m[i][j] = 0 // 자기 자신 곱셈은 비용x
* 점화식: m[i][j] = min_{i<=k<=j} ( m[i][k] + m[k+1][j] + p[i-1] * p[k] * p[j] ) // i<=k<=j인 모든 k 대해서 중 최솟값
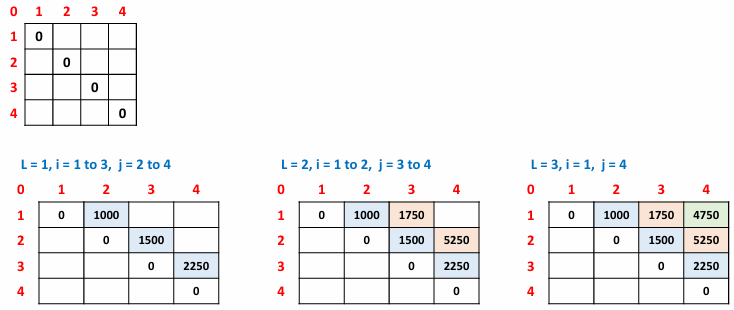
예시 계산
1. L = 1 (부분 행렬 길이 1)
m[1][2] = 10*20*5 = 1000. // 이 결과는 10*5 행렬이다
m[2][3] = 20*5*15 = 1500.
m[3][4] = 5*15*30 = 2250.
2. L = 2 (부분 행렬 길이 2)
m[1][3] = min(m[1][1] + m[2][3] + 10*20*15, m[1][2] + m[3][3] + 10*5*15) = min(4500, 1750) = 1750
m[2][4] 도 계산하면 5250
3. L = 3 (부분 행렬 길이 3)
m[1][4] = min(m[1][1] + m[2][4] + 10*20*30, m[1][2] + m[3][4] + 10*5*30, m[1][3] + m[4][4] + 10*15*30) = 4750
각 계산값 이차원배열에 아래와 같이 저장됨. m[1][4] 구하기 완료!
자료구조 자료
최소 비용 신장 트리 - 크루스칼, 프림
최소비용 신장트리= Minimum Spanning Tree
크루스칼, 프림, 다익스트라는 그리디 알고리즘: 각 단계에서 최선의 선택하는것을 반복하다보면 최종적인 해답에 도달하게됨. 플로이드만 DP
신장트리: 그래프 나의 모든 정점을 포함하는 트리. n개 정점->n-1개 간선.
최소비용신장트리 MST: 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결.
Kruskal의 MST 알고리즘
* 그래프의 edge들을 비용의 오름차순으로 정렬한다. edge들을 순서대로 검사해가며 최소비용신장트리에 하나씩 삽입해간다. (사이클이 생기지 않으면 포함, 그렇지 않으면 건너뛴다) 총 n-1개의 edge가 포함되면 MST가 완성된 것이다.
* parnet 배열을 사용한다. 크루스칼은 작은 신장트리 여러개. union find 알고리즘으로 노드가 어떤 트리에 속하는지 확인 (루트 노드를 확인) 같으면 cycle 생겨서 연결하면 안됨
Prim의 MST 알고리즘
* 시작 정점에서부터 출발하여 신장 트리를 단계적으로 키워 나감. 선택되는 간선들은 하나의 트리에 속함. 신장 트리 집합에 인접한 정점 중 최저 간선으로 연결된 정점 선택해 신장 트리 집합에 추가함.
간선 적은 희소그래프 경우 크루스칼 유리, 간선 많은 밀집그래프 경우 프림 유리
최단경로
All Pairs Shortest Path Problem 모든 경로쌍에 대해 찾는것은 플로이드
플로이드: Ak[i][j]: 그 배열의 i행 j열에 있는 값
'Subjects > 컴퓨터알고리즘' 카테고리의 다른 글
| [컴퓨터알고리즘] 13.2. 그리디 알고리즘 - 허프만 압축 (0) | 2024.06.20 |
|---|---|
| [컴퓨터알고리즘] 13. 그리디 알고리즘 (0) | 2024.06.20 |
| [컴퓨터알고리즘] 11. 레드블랙트리 (0) | 2024.06.19 |
| [컴퓨터알고리즘] 10. 이진검색트리 (0) | 2024.06.19 |
| [컴퓨터알고리즘] 5장 - 힙 정렬 (0) | 2024.04.24 |

