| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- bastion host
- AWS
- UNIDEV
- 생활코딩
- Route53
- 오블완
- UNICON
- 프로그래밍
- 전국대학생게임개발동아리연합회
- 인프라
- 42서울
- 티스토리챌린지
- VPC
- 프리티어
- 도커
- UNICON2023
- 스프링부트
- 체크인미팅
- EC2
- 라피신
- 게임개발동아리
- CICD
- 인디게임
- 온라인테스트
- 자바개발자
- 개발공부
- NAT gateway
- 백엔드개발자
- 백엔드
- 위키북스
- Today
- Total
Hyun's Wonderwall
[컴퓨터알고리즘] 14. 그래프 본문
그래프 G = (V,E)
- 정점 V, 간선 E.
- 무방향, 방향 그래프
- 차수: 인접 간선의 개수 (방향: in-degree, out-degree / 무방향: degree)
- weighted graph 가중치 그래프
- connected graph 연결 그래프. strongly connected 강연결 그래프.
- 희소 sparse, 밀집 dense
- 스택, 큐 그래프로 표현 가능
인접행렬 Adj[i][j]. Θ(V^2) 공간 필요
인접리스트 Adj[v] = {1, 2}. Θ(V+E) 공간 필요. 시간복잡도 O(n)
- 인접리스트 무방향이면 값 2번 있어야. 가중치그래프는 노드 (key,value) 로 구성.
- |adj[v]| = out-degree 갯수 (각 정점의 외차수의 개수만큼 인접노드.)
- 삭제랑 탐색 시에는 인접리스트가 O(n) 이지만 메모리측면과 그래프 순회시 인접리스트가 Θ(n+m)으로 우수. 굿.
Breath-First-Search (BFS) 폭 우선 탐색
- FIFO 큐 사용
- white, grey, black 노드
* BFS 수도코드
- BFS는 d[u]에 시작노드로부터의 거리를 저장한다.
BFS(G,s)
for each u ∈ V-{s} do # V에서 s 제외 정점들 초기화
color[u] <- WHITE
π[u] <- NIL; d[u] <- 무한대
color[s] = GRAY # s는 시작노드, 회색
π[s] <- NIL; d[s] = 0;
Q <- {s} # FIFO Q에 s 넣음
while Q != ∅ do
u <- DEQUEUE[Q]
for each v in Adj[u] do
if color[v] = WHITE then
color[v] = GRAY
π[v] <- u
d[v] <- d[u] + 1
ENQUEUE(Q,v) # 아직 탐색되지 않은 연결노드들 넣기
color[u] <- BLACK* BFS로 만들어지는 트리 BFT라고 칭함. '방향'이 부모-자식 연결로 바뀜.
BFS FIFO 큐 Q, vertex 프로세싱 직후 계산하기
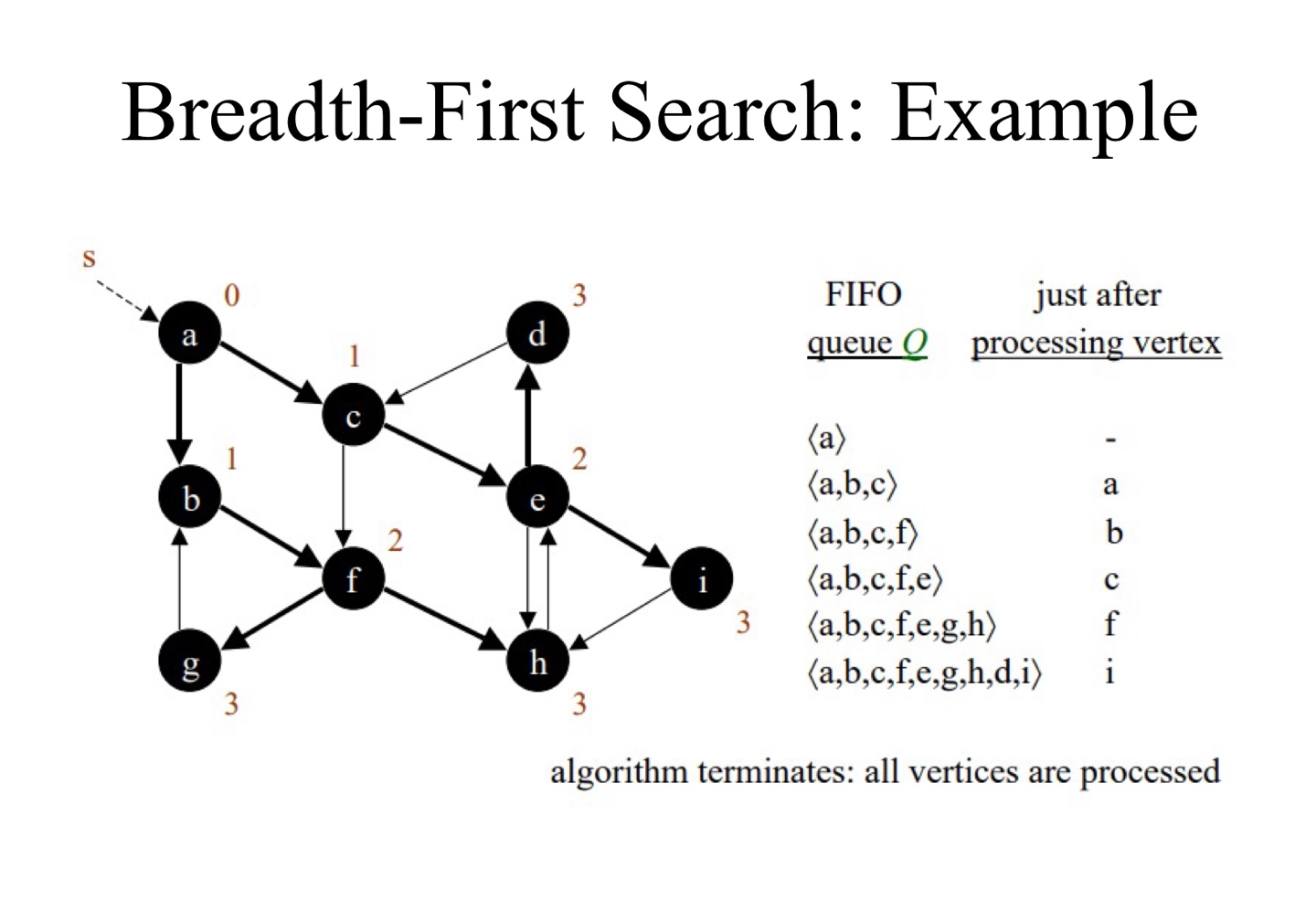
Depth-First Search (DFS) 깊이 우선 탐색
- 스택 사용
- white, grey, black 노드
- π(v) <- u 는 v의 부모노드가 u라는 뜻
- 시간복잡도 Θ(V+E)
DFS는 두 타임스탬프를 사용함: d[v], f[v]
- d[v]: 처음 발견되고 회색으로 칠해진 시간
- f[v]: 완료되고 검정으로 칠해진 시간
DFS 수도코드
DFS(G)
for each u∈V do
color[u] <- white
π[u] <- NIL
time <- 0 # 전역 시간
for each u∈V do
if color[u] = white
then DFS-VISIT(G,u)
DFS-VISIT(G,u)
color[u] <- gray
d[u] <- time <- time+1 # 1 증가시킨 time을 넣음
for each v∈Adj[u] do
if color[v] = white
π[u] <- u
DFS-VISIT(G,v)
color[u] <- black
f[u] <- time <- time+1
- DFS-VISIT 모든 정점 대해 한번만 호출됨
- 이 코드에서 u.color == black 지웠을때 DFS 유지? yes. white일때만 발견되지 않은 노드였으므로 탐색함. 회색/검정일때는 동일하게 동작함. f[u] <- time <- time+1가 저장되므로 방문완료상태 확인하는 코드를 추가할 수도 있음.
Directed Acyclic GraphTopological Sort 위상 정렬(끝나는 것 역순 나열)
'Subjects > 컴퓨터알고리즘' 카테고리의 다른 글
| [컴퓨터알고리즘] 15. 최소신장트리 (0) | 2024.06.20 |
|---|---|
| [컴퓨터알고리즘] 13.2. 그리디 알고리즘 - 허프만 압축 (0) | 2024.06.20 |
| [컴퓨터알고리즘] 13. 그리디 알고리즘 (0) | 2024.06.20 |
| [컴퓨터알고리즘] 12. 동적 프로그래밍 (0) | 2024.06.20 |
| [컴퓨터알고리즘] 11. 레드블랙트리 (0) | 2024.06.19 |


