| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- UNICON2023
- Spring boot
- 스프링부트
- NAT gateway
- 티스토리챌린지
- 캡스톤디자인프로젝트
- 체크인미팅
- EC2
- 라피신
- CICD
- UNIDEV
- openAI API
- 42서울
- 도커
- 백엔드개발자
- 인프라
- 전국대학생게임개발동아리연합회
- 오블완
- AWS
- 게임개발동아리
- 생활코딩
- 프로그래밍
- 개발공부
- 프리티어
- 프롬프트엔지니어링
- UNICON
- bastion host
- Route53
- spring ai
- Redis
- Today
- Total
Hyun's Wonderwall
[AIchemist] 파머완 - CH03. 평가 (1~5) 본문
AIchemist 1기
- 이화여대 머신러닝 입문 스터디
- 스터디 교재: 권철민, "파이썬 머신러닝 완벽 가이드"
- 2주차 과제: 파머완 p.145-p.172 (챕터3 섹션5까지)
[Chapter 03] 평가
머신러닝 프로세스: [데이터 가공/변환] -> [모델 학습/예측] -> [평가](예측을 잘 하고 있는지)
머신 러닝 모델은 여러가지 방법으로 예측 성능을 평가할 수 있음.
성능 평가 지표 - 모델이 [분류]냐 [회귀]냐에 따라 여러 종류.
회귀: 실제값과 예측값의 오차 평균값에 기반.
분류의 평가방법은 일반적으론 실제 결과 데이터와 예측 결과 데이터가 얼마나 정확하고 오류가 적게 발생하는가에 기반. 하지만 단순히 이러한 정확도만 가지고 판단했다가는 잘못된 평가 결과에 빠질 수 있음.
분류의 성능 평가 지표
- 정확도
- 오차행렬
- 정밀도
- 재현율
- F1 스코어
- ROC AUC
분류는 결정 클래스 값 종류의 유형에 따라 '이진 분류'와 '멀티 분류'로 나뉨.
이진 분류: 긍정/부정가 같은 2개의 결괏값만을 가짐
멀티 분류: 여러 개의 결정 클래스 값을 가짐
위에 언급한 분류의 성능 지표는 (이진/멀티 모두에 적용되지만) 이진 분류에서 더욱 중요하게 강조함.
3장에서는 0과 1로 결정값이 한정되는 이진 분류의 성능 평가 지표 위주로 알아본다.
1. 정확도
정확도 : 실제 데이터에서 예측 데이터가 얼마나 같은지를 판단하는 지표.
(정확도 Accuracy) = (예측 결과가 동일한 데이터 건수)/(전체 예측 데이터 건수)정확도는 직관적으로 모델 예측 성능을 나타내지만, 데이터 분포도가 균일하지 않은 경우 왜곡된 수치가 나타날 수 있는 것이 맹점.(너무 높은 등..)
불균형한 레이블 데이터 세트에서는 성능 지표로 사용하면 안 된다. 이러한 한계점 극복 위해 다른 여러가지 분류 지표와 함께 적용해서 성능을 평가해야 한다.
2. 오차 행렬
오차 행렬(confusion matrix, 혼동행렬) : 학습된 분류 모델이 예측을 수행하면서 얼마나 헷갈리고 있는지도 함께 보여주는 지표.
이진 분류의 예측 오류가 얼마인지 + 어떠한 유형의 예측 오류가 발생하고 있는지 함께 나타낸다. 이진 분류에서 성능 지표로 잘 활용됨.
4분면 행렬에서 실제 레이블 클래스 값과 예측 레이블 클래스 값이 어떠한 유형을 가지고 매핑되는지를 나타낸다
4분면의 왼쪽, 오른쪽 : 예측된 클래스 값 기준으로 - Negative와 Positive로 나눔
4분면의 위, 아래 : 실제 클래스 값 기준으로 - Negative와 Positive로 나눔
그러면 예측 클래스와 실제 클래스 값 유형에 따라 TN, FP, FN, TP 로 오차 행렬 4분면 채울 수 있음
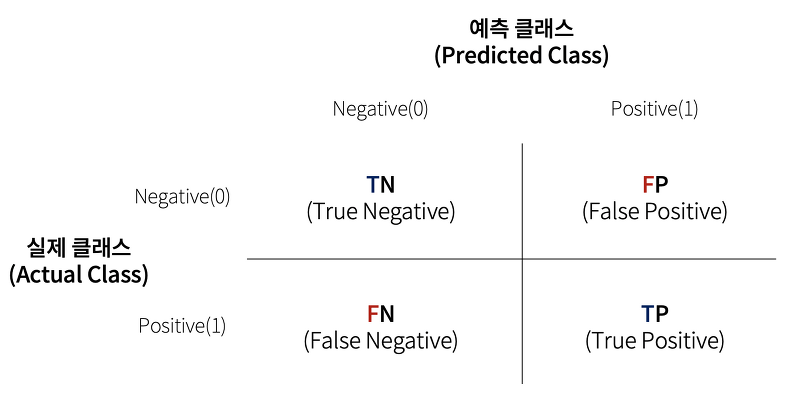
"정답+예측값"
True/False : 예측값과 실제값이 같은가/틀린가
Negative/Positive : 예측 결과 값이 부정(0)/긍정(1)
TN(True Negative) : 예측값을 Negative값(0)으로 예측했고 실제 값 역시 Negative값(0), 정답이므로 True
FP(False Positive) : 예측값을 Positive값(1)로 예측했는데 실제 값은 Negative값(0), 틀렸으므로 False
FN(False Negative) : 예측값을 Negative값(0)으로 예측했는데 실제 값은 Positive값(1), 틀렸으므로 False
TP(True Positive) : 예측값을 Positive값(1)로 예측했고 실제 값 역시 Positive값(1), 정답이므로 True
오차 행렬 구하는 사이킷런 API : confusion_matrix( )
예측 결과와 실제 결과를 인자로 입력해 오차 행렬을 배열 형태로 출력.
출력한 오차 행렬은 ndarray 형태
TN, FP, FN, TP 값을 조합해 Classifier 성능을 측정할 수 있는 주요 지표인 정확도(Accuracy), 정밀도(Precision), 재현율(Recall) 값을 알 수 있다.
*정확도 : 오차 행렬에서 True에 해당하는 값인 TN, TP에 좌우됨
정확도 = (TN+TP)/(TN+FP+FN+TP)
불균형한 레이블 클래스를 가지는 이진 분류 모델에서는
많은 데이터 중에서 중점적으로 찾아야 하는 매우 적은 수의 결과값에 Positive를 설정해 1값을 부여하고 그렇지 않은 경우 Negative로 0값을 부여하는 경우가 많음.
이때 Positive 데이터 건수가 매우 작기 떄문에 데이터에 기반한 ML 알고리즘은 Positive보다는 Negative로 예측 정확도가 높아지는 경향 발생
결과적으로 Negative에 대한 예측 정확도만으로 분류 정확도가 매우 높게 나타나는 수치적인 반단 오류 발생...
불균형한 데이터 세트에서 더 선호되는 평가 지표인 정밀도와 재현율에 대해 알아보자.
3. 정밀도와 재현율
정밀도 : 예측을 Positive로 한 것 중(TP, FP) 실제값이 Positive인 것(TP)
*Negative(FP)->Positive 오판단이 더 영향이 클 때
재현율 : 실제값이 Positive인 대상 중(FN, TP) 예측과 실제값이 Positive로 일치한 것(TP)
*Positive(FN) ->Negative 오판단이 더 영향이 클 때
정밀도 = TP / (FP+TP)
재현율 = TP / (FN+TP)
재현율이 중요 지표인 경우: 실제 Positive 데이터를 Negative로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우 (암 진단 등)
3.1. 정밀도/재현율 트레이드오프
정밀도와 재현율은 상호 보완적인 평가 지표여서 어느 한 쪽을 강제로 높이면 다른 하나의 수치가 떨어지기 쉬움.
임계값 낮추면 P 높아지고 N 낮아짐 -> 재현율 증가, 정밀도 감소
임계값 높이면 N 높아지고 P 낮아짐 -> 정밀도 증가, 재현율 감소
3.2. 정밀도와 재현율의 맹점
Positive 예측의 임계값을 변경함에 따라 정밀도와 재현율의 수치가 변경됨.
정밀도와 재현율은 상호 보완적인 평가 지표.
임계값의 변경은 업무 환경에 맞게 두 개의 수치를 상호 보완할 수 있는 수준에서 적용돼야 함
정밀도가 100%가 되는 방법
확실한 경우만 Positive로 예측하고 나머지는 모두 Negative로 예측한다
정밀도 = TP/(TP+FP), 확실한 Positive만 Positive로 예측하고 나머지는 모두 Negative로 예측한다면 TP는 1, FP는 0이므로 정밀도는 1/(1+0)=100%.
재현율이 100%가 되는 방법
모든 환자를 Positive로 예측한다.
재현율 = (TP)/(TP+FN) 에서 FN이 0이므로 100%...
문제: 이처럼 정밀도와 재현율 성능 수치도 어느 한 쪽만 참조하면 극단적인 수치 조작이 가능함. 따라서 정밀도 또한 재현율 중 하나는 스코어가 좋고 하나는 스코어가 나쁜 분류는 성능이 좋지 않은 분류임.
정밀도와 재현율 중 하나만 강조되어서는 안 됨.
정밀도와 재현율의 수치가 적절하게 조합돼 분류의 종합적인 성능 평가에 사용될 수 있는 평가 지표가 필요함.
4. FI 스코어
F1 스코어 : 정밀도와 재현율을 결합한 지표
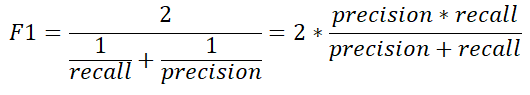
F1 스토어를 구하기 위한 API : f1_score( )
이를 이용해 정밀도와 재현율 절의 예제에서 학습/예측한 로지스틱 회귀 기반 타인타닉 생존자 모델의 F1 스코어를 구해보는 실습 진행.
그리고 임곗값을 변화시키면서 평가 지표를 구해 보자
get_clf_eval() 함수에 구하는 로직 추가
get_clf_by_threshold( ) 이용해 임곗값 0.4~0.6
테스트 해보니 임곗값이 0.6일 때 재현율이 크게 감소했다(주의!)
5. ROC 곡선과 AUC
이진 분류 예측 성능 측정에서 중요하게 사용되는 지표
ROC 곡선 : (뜻을 번역하면 수신자 판단 곡선)
FPR(False Positive Rate)이 변할 때 TPR(True Positive Rate)이 어떻게 변하는지를 나타내는 곡선
FPR을 X축으로, TPR을 Y축으로 잡으면 FPR의 변화에 따른 TPR의 변화가 곡선 형태로 나타난다.
*ROC 곡선 메소드: roc_curve( )
TPR(True Positive Rate) : 재현율 = TP/(FN+TP)
FPR = 1 - TNR*
*TNR : 민감도 = TN/(FP+TN)
ROC 곡선은 FPR과 TPR의 변화 값을 보는 데 이용.
분류의 성능 지표에 사용되는 것은 AUC 값으로 결정.
AUC(Area Under Curve) 값 : ROC 곡선 밑의 면적을 구한 것, 1에 가까울수록 좋은 수치.
AUC 수치 커지려면 FPR이 작은 상태에서 얼마나 큰 TPR을 얻을 수 있느냐가 관건.
보통의 분류는 0.5이상의 값을 가짐.
get_clf_eval( )함수에 roc_auc_score( )을 추가해 ROC AUC값을 측정하는 로직을 추가하기
* ROC AUC는 예측 확률값 기반 계산 -> get_clf_eval( ) 함수의 인자로 받을 수 있도록 함수형 아래와 같이 변경
get_clf_eval(y_test, pred=None, pred_proba=None)
=> 정확도, 정밀도, 재현율, F1스코어, ROC AUC 값까지 출력 가능
def get_clf_eval(y_test, pred_None, pred_proba=None):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_Score(y_test, pred)
f1 = f1_score(y_test, pred)
f1 = f1_score(y_test, pred)
# ROC-AUC 추가
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion)
# ROC-AUC print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2: .4f}, F1: {3:.4f}, AUC: {4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))'Study > Python-Machine-Learning' 카테고리의 다른 글
| [AIchemist] 파머완 - CH04. 분류 (5~8, 11) (1) | 2023.10.10 |
|---|---|
| [AIchemist] 파머완 - CH03. 평가 (6. 피마 인디언 당뇨병 예측) (0) | 2023.10.09 |
| [AIchemist] 파머완 - CH02. 사이킷런으로 시작하는 머신러닝 (6. 사이킷런으로 수행하는 타이타닉 생존자 예측) (0) | 2023.09.25 |
| [AIchemist] 파머완 - CH02. 사이킷런으로 시작하는 머신러닝 (1~5) (0) | 2023.09.19 |
| [AIchemist] 파머완 - CH01. 파이썬 기반의 머신러닝과 생태계 이해 (4. 데이터 핸들링 - 판다스) (0) | 2023.09.19 |


