| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 개발공부
- AWS
- 게임개발동아리
- 스프링부트
- 생활코딩
- openAI API
- 프리티어
- Redis
- CICD
- 인프라
- Spring boot
- EC2
- bastion host
- 프로그래밍
- UNICON2023
- 전국대학생게임개발동아리연합회
- 도커
- Route53
- 체크인미팅
- 오블완
- NAT gateway
- spring ai
- 티스토리챌린지
- UNICON
- 캡스톤디자인프로젝트
- 42서울
- 백엔드개발자
- UNIDEV
- 프롬프트엔지니어링
- 라피신
- Today
- Total
Hyun's Wonderwall
[AIchemist] 파머완 - CH04. 분류 | 10. 캐글 신용카드 사기 검출 본문
[AIchemist] 파머완 - CH04. 분류 | 10. 캐글 신용카드 사기 검출
Hyun_! 2023. 10. 31. 08:3910. 캐글 신용카드 사기 검출
- Kaggle 신용카드 데이터 세트 https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud
- 해당 데이터 세트의 레이블인 Class 속성은 매우 불균형한 분포를 가짐.
- Class는 0과 1로 분류되는데, 0: 신용카드 정상 트랜잭션 / 1: 신용카드 사기 트랜잭션
- 전체 데이터의 0.172%만이 사기(레이블 값 1)
+ 사기 검출(Fraud Detection), 이상 검출(Anomaly Detection)과 같은 데이터 세트는 이처럼 레이블 값 극도로 불균형한 분포 가지기 쉬움.
언더 샘플링과 오버 샘플링의 이해
- 레이블이 불균형 분포인 데이터 세트를 학습시킬 때 예측 성능의 문제가 발생할 수 있음.
(이상 레이블을 가지는 데이터 건수가 정상 레이블을 가진 데이터 건수에 비해 너무 적으면->제대로 다양한 유형 학습 불가, 정상 레이블 가지는 데이터 건수 매우 많아 정상 레이블로 치우친 학습을 수행->제대로 된 이상 데이터 검출 어려워짐)
- 지도학습에서 극도로 불균형한 레이블 값 분포로 인한 문제점 해결 위해서는 적절한 학습 데이터를 확보하는 방안이 필요: 오버 샘플링과 언더 샘플링 (*오버 샘플링이 예측 성능상 조금 유리한 경우가 많아 더 많이 사용됨)
*언더 샘플링: 많은 레이블 가진 데이터 세트를 ➔ 적은 레이블 가진 데이터 세트 수준으로 감소
ex: 정상이 1만건, 이상이 1백건일 때 정상을 1백건으로 줄여버림. 이러면 과도하게 정상 레이블로 학습/예측하는 부작용을 개선할 수 있지만, 너무 많은 정상 레이블 데이터를 감소시켜 정상 레이블이 제대로 학습을 수행할 수 없는 문제가 발생할 수도 있으니 유의
*오버 샘플링: 적은 레이블 가진 데이터 세트를 ➔ 많은 레이블 가진 데이터 세트 수준으로 증식
동일한 데이터 단순 증식x(그러면 과적합), 원본 데이터의 피처 값들을 아주 약간 변경해서 증식시킴.
대표적으로 SMOTE*(Synthetic Minority Over-sampling Technique) 방법이 있음
*SMOTE 수행 절차: 적은 데이터 세트에서 개별 데이터들의 K 최근접 이웃을 찾아서, 이 데이터와 K개 이웃들의 차이를 일정 값으로 만들어서 기존 데이터와 약간 차이나는 새로운 데이터를 생성.
- 파이썬 패키지 imbalanced-learn이 SMOTE를 구현함. 아나콘다로 설치.
데이터 일차 가공 및 모델 학습/예측/평가
# 데이터 세트 로딩, 신용카드 사기 검출 모델 생성

Time 피처는 큰 의미 없으니 제거한다
Amount 피처는 신용카드 트랜잭션 금액을 의미
Class는 레이블, 0인 경우 정상이고 1인 경우 사기
card_df.info()로 확인해보면 284,807개의 레코드에서 결측치(Missing Value)는 없으며 Class 레이블만 int형이고 나머지는 모두 float형이다.
# 이번 실습 목표: 보다 다양한 데이터 사전 가공 수행, 이에 따른 예측 성능도 함께 비교
- preprocessed_df() : 인자로 입력된 DataFrame을 복사한 뒤, 이를 가공하여 반환
- get_train_test_df() : 데이터 가공 후 학습/테스트 데이터 세트를 반환
from sklearn.model_selection import train_test_split
# 인자로 입력받은 DataFrame을 복사 한 뒤 Time 컬럼만 삭제하고 복사된 DataFrame 반환
def get_preprocessed_df(df=None):
df_copy = df.copy()
df_copy.drop('Time', axis=1, inplace=True)
return df_copy
# get_train_test_dataset()은 get_processed_df() 호출한 뒤 학습 피처/레이블 데이터 세트, 테스트 피처/레이블 세트를 반환함
- get_train_test_dataset()은 내부에서 train_test_split() 함수를 호출하며, 테스트 데이터 세트를 전체의 30%인 Stratified 방식으로 추출해 학습 데이터와 테스트 데이터 세트의 레이블 값 분포도를 서로 동일하게 만듬
# 사전 데이터 가공 후 학습과 테스트 데이터 세트를 반환하는 함수.
def get_train_test_dataset(df=None):
# 인자로 입력된 DataFrame의 사전 데이터 가공이 완료된 복사 DataFrame 반환
df_copy = get_preprocessed_df(df)
# DataFrame의 맨 마지막 컬럼이 레이블, 나머지는 피처들
X_features = df_copy.iloc[:, :-1]
y_target = df_copy.iloc[:, -1]
# train_test_split( )으로 학습과 테스트 데이터 분할. stratify=y_target으로 Stratified 기반 분할
X_train, X_test, y_train, y_test = \
train_test_split(X_features, y_target, test_size=0.3, random_state=0, stratify=y_target)
# 학습과 테스트 데이터 세트 반환
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
# 생성한 학습 데이터 세트와 테스트 데이터 세트의 레이블 값 비율 백분율로 환산해서 서로 비슷하게 분할됐는지 확인

# 모델 만들기: 로지스틱 회귀와 LightGBM 기반의 모델이 데이터 가공을 수행하면서 예측 성능이 어떻게 변하는지 살펴볼 것임. [재현율(Recall), ROC_AUC] 보기
1) 로지스틱 회귀 이용해 예측: (3장에서 생성한) get_clf_eval() 함수 재활용, 테스트 데이터 세트로 측정.
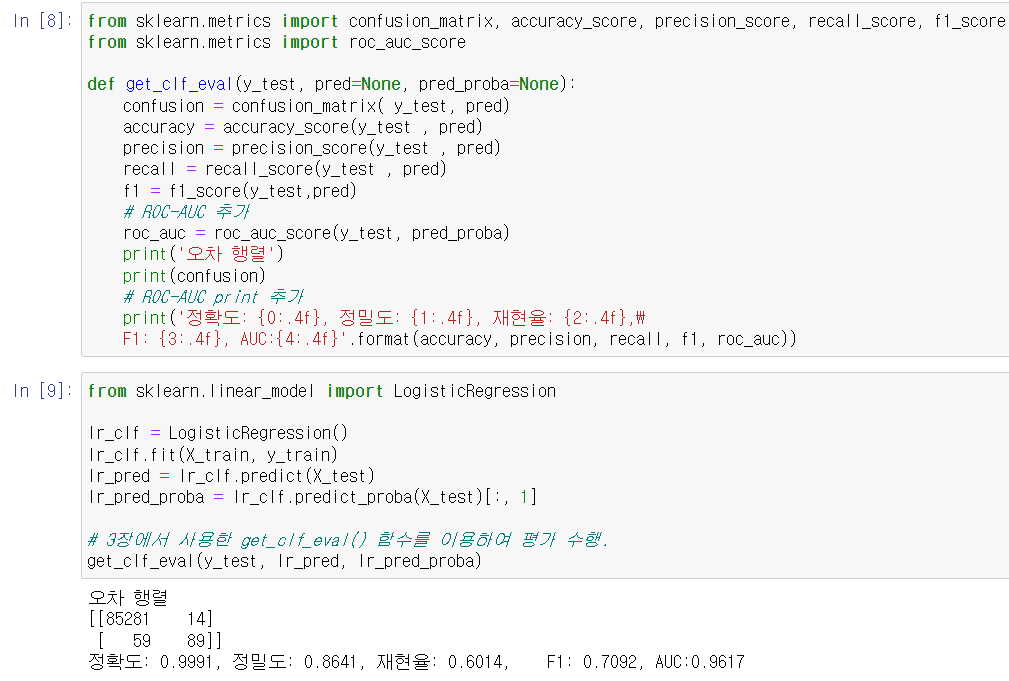
2) LightGBM 이용해 모델 만들고 예측:
- 이 데이터 세트는 극도로 불균형한 레이블 값 분포를 가지고 있으므로 LGBMClassifier 객체 생성 시 boost_from_average=False로 파라미터를 설정해야 한다. (*주의: 최근 버전에서 LightGBM의 boost_from_average 파라미터 디폴트값이 True인데, 이 예제처럼 레이블값이 극도로 불균등한 분포인 경우 True로 놔두면 재현율 및 ROC_AUC 성능이 매우 크게 저하된다. boost_from_average=False로 파라미터 설정하기)
- LightGBM으로 모델 학습한 뒤 별도의 테스트 데이터 세트에서 예측 평가를 수행

데이터 분포도 변환 후 모델 학습/예측/평가
왜곡된 분포도를 가지는 데이터를 재가공한 뒤 모델을 다시 테스트할 것임.
먼저, creditcard.csv의 중요 피처 값의 분포도를 살펴본다.
- 로지스틱 회귀는 선형 모델이고, 대부분의 선형 모델은 중요 피처들의 값이 정규 분포 형태를 유지하는 것이 선호함.
- Amount 피처는 신용 카드 사용 금액으로 정상/사기 트랜잭션을 결정하는 매우 중요한 속성일 가능성이 높음
# Amount 피처 분포도 확인해 보자
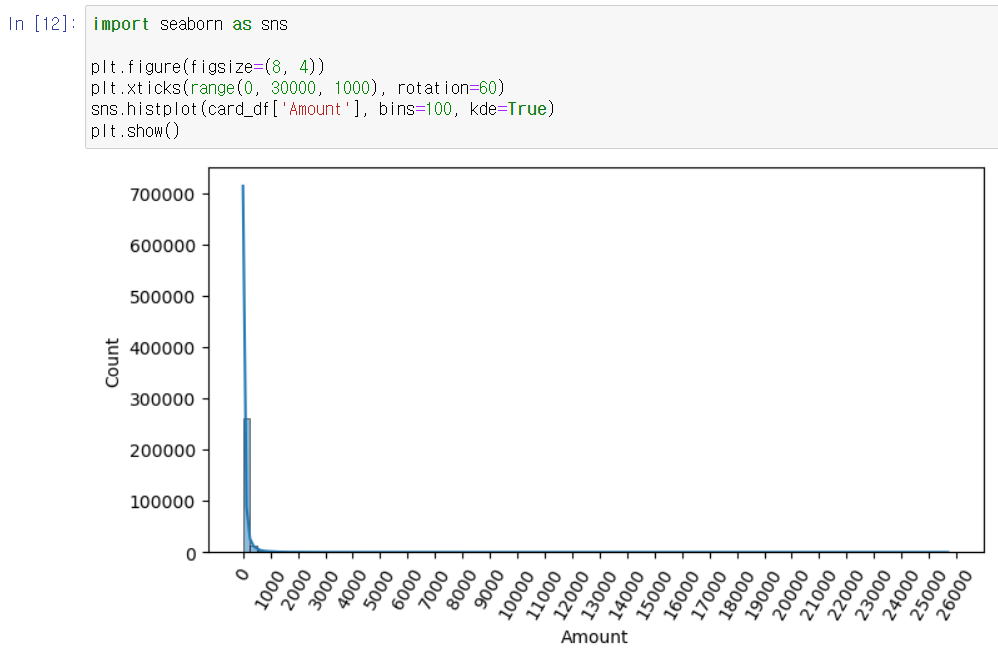
# Amount를 표준 정규 분포로 변환한 뒤 로지스틱 회귀의 예측 성능을 측정
- 데이터 가공 함수 get_processed_df() 코드를 변경: StandardScaler 클래스를 이용해 Amount 피처를 정규 분포 형태로 변환함.
- (1) 코드 수정 후 get_train_test_dataset()을 호출해 학습/테스트 데이터 세트를 생성, (2) get_model_train_eval()을 이용해 로지스틱 회귀와 LigthGBM 모델을 각각 학습/예측/평가.

정규 분포 형태로 Amount 피처값을 변환한 후 테스트 데이터에 적용하니
- 로지스틱 회귀: 정밀도와 재현율이 오히려 조금 저하됨
- LightGBM: 정밀도와 재현율이 약간 저하되었지만 큰 성능성의 변경은 없음 //음??
# 로그 변환 수행해 보기
- 로그 변환은 데이터 분포도가 심하게 왜곡되어 있을 경우 적용할 수 있는 중요 기법 중 하나. 원래 값을 log 값으로 변환해 원래 큰 값을 상대적으로 작은 값으로 변환하기 때문에 데이터 분포도의 왜곡을 상당히 개선함. (5장에서 자세히...)
- 로그 변환은 넘파이의 log1p()함수를 이용한다.
- (1) 데이터 가공 함수 get_processed_df()를 로그 변환 로직으로 변경, (2) Amount 피처를 로그 변환한 후 다시 로지스틱 회귀와 LIghtGBM 모델을 적용하여 예측 성능 확인.
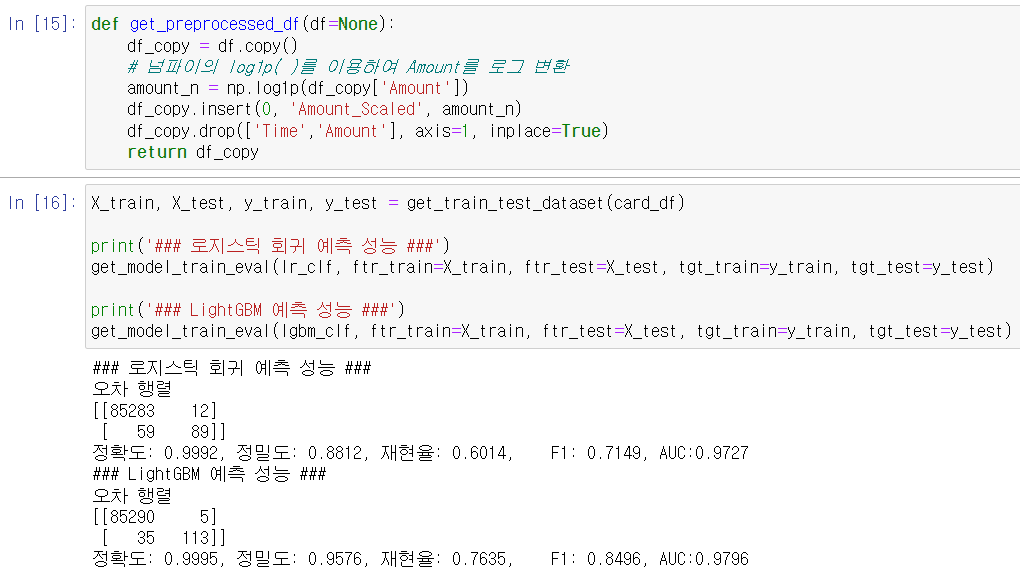
로지스틱 회귀의 경우 원본 데이터 대비 정밀도는 향상되었지만 재현율은 저하됨.
LightGBM의 경우 재현율이 향상됨.
*결론: 레이블이 극도로 불균일한 데이터 세트에서 로지스틱 회귀가 데이터 변환 시 약간의 불안정한 성능 결과를 보여주고 있음.
이상치 데이터 제거 후 모델 학습/예측/평가
이상치 데이터(아웃라이어, Outlier): 전체 데이터의 패턴에서 벗어난 이상 값을 가진 데이터. 이상치로 인해 성능에 영향 받는 경우가 발생하기 쉬움.
이러한 이상치를 찾아낸 후 이상치 데이터를 제거한 뒤에 다시 모델을 평가해 보자.
이상치를 찾는 방법 중 IQR(Inter Quantile Range) 방식을 적용해보자.
IQR: 사분위 값의 편차를 이용하는 기법. 흔히 Box Plot 방식으로 시각화할 수 있다.
*사분위란? 전체 데이터를 값이 높은 순으로 정렬하고, 이를 1/4씩 구간을 분할하는 것.
0 ----- Q1(25%) ----- Q2(50%) ----- Q3(75%) ----- Q4(100%)
이때 Q1~Q3의 범위를 IQR이라고 한다.
IQR을 이용해 이상치 데이터 검출하는 방식: IQR에 1.5를 곱해서 생성된 범위를 이용해 최댓값과 최솟값을 결정한 뒤 최댓값을 초과하거나 최솟값에 미달하는 데이터를 이상치 로 간주함 (*디폴트가 1.5)
* 일반적인 데이터가 가질 수 있는 최댓값: 3/4분위수(Q3)에서 IQR*1.5를 더한 지점
* 일반적인 데이터가 가질 수 있는 최솟값: 1/4분위수(Q1)에서 IQR*1.5를 뺀 지점
이상치: 이렇게 결정된 최댓값보다 큰 값 또는 최솟값보다 작은 값.
IQR 방식을 시각화한 도표가 Box Plot. (박스 플롯은 사분위 편차, IQR, 이상치를 나타냄)
# 직접 이상치 데이터를 IQR 이용해 제거하기
- 먼저 어떤 피처의 이상치 데이터를 검출할 건지 선택 필요.
- 매우 많은 피처가 있을 경우 이들 중 결정값(즉 레이블)과 가장 상관성이 높은 피처들을 위주로 이상치를 검출하는 것이 좋음. 모든 피처들의 이상치 검출하는 것은 시간이 많이 소모되고, 결정값과 상관성 높지 않은 피처들 경우는 이상치를 제거하더라도 크게 성능 향상 x
# DataFrame의 corr()을 이용해 각 피처별로 상관도를 구한 뒤 시본의 heatmap을 통해 시각화해보자

<상관관계 히트맵> cmap을 'RdBu'로 설정함
- 양의 상관관계가 높을수록 색깔이 진한 파란색, 음의 상관관계가 높을수록 색깔이 진한 빨간색에 가깝
- 상관관계 히트맵에서 맨 아래에 위치한 결정 레이블인 Class 피처 와음의 상관관계가 가장 높은 피처는 V14와 C17이다.
#이 중 V14에 대해서만 이상치 찾아서 제거해보기
- IQR 이용해 이상치를 검출하는 함수를 생성한 뒤 이를 이용해 이상치를 삭제.
- get_outlier() 함수는 인자로 DataFrame과 이상치를 검출한 칼럼을 입력받음. 함수 내에서 넘파이의 percentile()을 이용해 1/4분위와 3/4분위를 구하고, 이에 기반에 IQR을 계산한다. 계산된 IQR에 1.5를 곱해서 최댓값과 최솟값 범위를 구한 뒤, 최댓값보다 크거나 최솟값보다 작은 값을 이상치로 설정하고 해당 이상치가 있는 DataFrame Index를 반환한다.
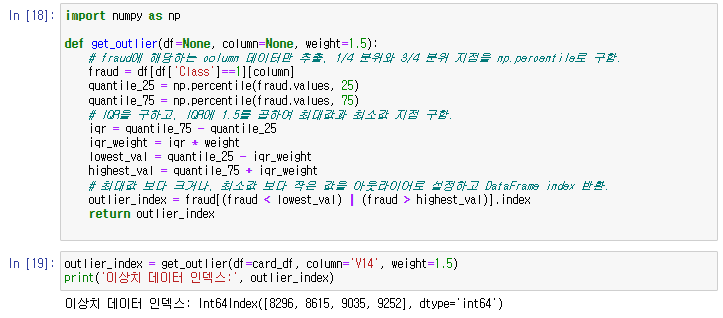
- get_outlier()함수를 이용해 V14칼럼에서 이상치 데이터를 찾아보니 총 4개의 데이터가 이상치로 추출됨.
# get_outlier()를 이용해 이상치를 추출하고 이를 삭제하는 로직을 get_processed_df()함수에 추가 데이터를 가공한 뒤 이 데이터 세트를 이용해 로지스틱 회귀와 LightGBM 모델을 적용해본다

- 이상치 데이터를 제거한 뒤 로지스틱 회귀와 LightGBM 모두 예측 성능이 크게 향상되었다.
로지스틱 회귀의 경우 재현율이 60.14%에서 67.12%로 크게 증가했으며 LightGBM의 경우도 76.35%에서 82.88%로 크게 증가했다.
SMOTE 오버 샘플링 적용 후 모델 학습/예측/평가
SMOTE기법으로 오버 샘플링을 적용한 뒤 로지스틱 회귀와 LightGBM 모델의 예측 성능을 평가해 본다
SMOTE는 앞에서 설치한 imbalanced-learn 패키지의 SMOTE 클래스를 이용해 간단하게 구현이 가능함
SMOTE를 적용할 때는 반드시 학습 데이터 세트만 오버 샘플링을 해야 한다. 검증or테스트 데이터 세트를 오버 샘플링할 경우 결국은 원본 데이터 세트가 아닌 데이터 세트에서 검증 또는 테스트를 수행하기 때문에 올바른 검증/테스트가 될 수 없다.
앞 예제에서 생성한 학습 피처/레이블 데이터 세트를 SMOTE 객체의 fit_resample() 메서드를 이용해 증식한 뒤 데이터를 증식 전과 비교해 본디
'Study > Python-Machine-Learning' 카테고리의 다른 글
| [AIchemist] 파머완 - CH05. 회귀 | 9. 회귀 실습 - 자전거 대여 수요 예측 (0) | 2023.11.07 |
|---|---|
| [AIchemist] 파머완 - CH05. 회귀 | 1~8 (0) | 2023.11.07 |
| [AIchemist] 파머완 - CH04. 분류 | 09. 캐글 산탄데르 고객 만족 예측 (0) | 2023.10.31 |
| [AIchemist] 파머완 - CH04. 분류 (5~8, 11) (1) | 2023.10.10 |
| [AIchemist] 파머완 - CH03. 평가 (6. 피마 인디언 당뇨병 예측) (0) | 2023.10.09 |



